The binary we'll be analysing in this tutorial is none other than Challenge 9 from the Flare-On challenge by Fireeye. For those of you who've never heard of it, it's a CTF-style Reverse Engineering challenge. This year, Fireeye has created 11 challenges each of which contain an e-mail address used to obtain the next binary.
Compared to the previous binary we've tackled, this will be much more involving but hang in there, the greater the obstacle the more glory in overcoming it. The operations used by the program to hide the answer are not particularly complicated but there are various anti-disassembly techniques we need to overcome. Fortunately for us there's only 2 very important ASM instructions we need to cover before we start.
Download binary here.
The Compare and Exchange operator compares the accumulator (
In this tutorial I'll be using IDA once again. Originally I've solved this challenge using Immunity Debugger since IDA kept moaning and groaning about instructions changing during execution. (You'll see what I meant by that statement). Before that though, let's run the program:
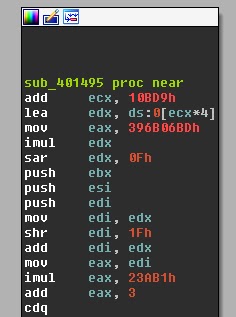
In the functions window, IDA identifies a very complicated but interesting-looking function, sub_401495:
At first glance it seems that we've identified the core function of the program. Guess what? Forget about the function. The code is never reached! This wasted me quite some time during the challenge. When dealing with self-modifying code, static analysis is no good. Having said that, if there's anyone who's got an idea on how to unroll self-modifying code for static analysis, please step forward. Thanks in advance.
While single-stepping through the program there will be times where the Instruction Pointer points to a section which has been interpreted as data such as the following:
If this happens, press "c" to directly convert that part to code. IDA might prompt you for confirmation; press "YES". We can now see that the section makes much more sense:
As if it weren't bad enough, the binary is full of self-modifying code and "conditional" jumps all over the place. Consider the following:
The last line diverts the flow to another location if the Zero Flag is set, but
A good practice when debugging is to set some well-placed breakpoints. For this binary it's easier said than done since we're not guaranteed that the instructions remain consistent throughout execution. We have no choice but to start from the top. We run the program with the "Suspend on process entry point" option set, which is found under "Debugger Setup". This will force the program to halt on the very first instruction. The start of the program looks like this :
While holding F7 (single-stepping) down, we keep an eye on the stack. The program goes through several transformations before it even reaches the point where it asks us to input the password. After some time we get the following stack setup:
At the top we notice a kernel32_WriteFile system call and a pointer to the data section, .data:aIHaveEvolvedSi, which holds the string "I have evolved since the first challenge. You have not. Bring it.". This is followed by a kernel32_ReadFile call and 41 pointers to .text:00401736. The bottom 31 pointers are not shown in the image. This should look familiar as it's the real starting point. It writes the welcoming message to the console, reads our input and .. hmm .. executes some function 41 times. At this point we're not sure what this function does so let's investigate further by setting a breakpoint at address 0x00401736.
We continue the execution (F9), input a random password in the console and hit enter. The program stops at the breakpoint. This happens everytime we try and continue for 41 times after which the program displays the friendly "You are failure" message. Let's look closely at what happens at each iteration of this mysterious function.
It's time to start filtering the nonsense and identify the operations that matter; those that actually operate on our input, or are influenced by it. We run the program with different passwords to hopefully elicit some change in the program's execution flow. The following is a list of instructions that are affected by our input in each iteration of the function:
So finally we're left with a simple formula that contains 4 unknowns, 3 of which can be gathered by going through each function, and our input. Let's change the subject of the constructed formula to
I admit that this tutorial is quite a leap from the previous ones. Don't get disheartened though!!
For those of you who would like to take a go at the other challenges, Fireeye has made the binaries available for download here. Personally I quite enjoyed them and even though they can be quite frustrating at times, I've definitely learnt a lot .. それでは、また
x86 Instructions
CMPXCHG
The Compare and Exchange operator compares the accumulator (
AL/AX/EAX) to the first operand. If equal, the first operand (Destination) is loaded with the second (Source). If not, the accumulator is loaded with first operand (Destination). Programmatically it looks something like this:
if (Accumulator == Destination) {
ZF = 1;
Destination = Source;
}
else {
ZF = 0;
Accumulator = Destination;
}
Let's look at some concrete examples:
cmpxchg ecx, edx ; if EAX = 0x05, ECX = 0x05 & EDX = 0x04 then, ECX = 0x04
; if EAX = 0x03, ECX = 0x05 & EDX = 0x04 then, EAX = 0x05
cmpxchg cx, dx ; same as above but for Words
cmpxchg [edi], si ; same as above but the Destination is a memory region
CMOVZ & CMOVNZ
CMOVZ stands for Conditional Move if Zero whereas CMOVNZ stands for Conditional Move if Not Zero. These instructions can move a value from memory to a register or from one register to another. Unlike the original MOV instruction, the source operand cannot be a memory region and immediate values are not allowed anywhere. Their description is self-explainatory but let's look at a few examples:
cmovnz eax, ebx ; if ZF = 0, EAX = EBX, else nothing
cmovnz eax, [ebx] ; if ZF = 0, EAX = [EBX], else nothing
cmovz eax, ebx ; if ZF = 1, EAX = EBX, else nothing
cmovz eax, [ebx] ; if ZF = 1, EAX = [EBX], else nothing
Basically a move occurs if the condition is satisfied, else the move is not performed. Many other conditional move statements exist but since we'll only encounter 1 of them in the binary, and also because in my experience they're not that common, I won't be covering them, at least this time.
The Binary
Command Prompt
C:\>you_are_very_good_at_this.exe
I have evolved since the first challenge. You have not. Bring it.
Enter the password> lets_try_our_luck
You are failure
C:\>
Wow that's harsh!! The binary accepts a password, validates it in some way, and outputs a failure or success (maybe?) message. Guessing and brute-forcing is not going to get us anywhere so let's load the program in IDA and start debugging.
Your eyes can deceive you, don't trust them
XOR EAX, EAX is always zero, hence ZF is always set. Also what's this loc_401A54+2? Why not loc_401A56? This happens when the code pointed to by this instruction has been messed up and/or wasn't interpreted correctly. Jumping to it and pressing "c" should clear things up.
Finding our way round the maze
All that glitters is not gold, it can be diamonds
- [0x00401A9C] mov al, [eax+ecx] - Loads a character from our input into
AL. - [0x0014FDB4] mov ah, [esp+ebx+0B4h] - Loads some byte into
AH. - [0x0014FDB8] xor al, ah -
XORs our character with this byte. - [0x0014FDB4] mov cl, [esp+ebx+88h] - Loads some byte into
CL. - [0x00401B14] rol al, cl - Performs a
ROLonAL,CLtimes. - [0x0014FDB8] cmpxchg bl, dl - Compares and Exchanges
BLwithDL, ifAL=BL, thenZF= 1, else 0. - [0x00401B3D] cmovnz esi, edx - If
ZF= 1,ESIremains 0, elseESI=EDX= 1. - [0x00401B49] xchg eax, esi - If
ESIwas 1, nowEAXis 1, and same for 0. - [0x0014FD88] cmpxchg bl, dl - At this point
BL= 0 andDL= 1 so ifAL= 0,BLbecomes 1, elseBLremains 0. - [0x00401B74] mov eax, ebx -
EAXnow holds the result, either a 1 or a 0.
EAX is either incremented or isn't, so which one is the right path? The answer lies at the end of the program:
If EAX is 0x29, i.e. 41, i.e. the number of iterations our favourite function executes, then jump to the "You are success" section, else jump to the "You are failure" section. Excellent !! We now know that for each iteration of the function, EAX has to be incremented. Let's look again at the 10 instructions listed above and, starting from the bottom, make our way up starting from the fact that EAX has to be 1:
- [0x00401B74] mov eax, ebx -
EAXhas to be 1, soEBXhas to be 1. - [0x0014FD88] cmpxchg bl, dl -
EBXhas to be 1, soALhas to be 0. - [0x00401B49] xchg eax, esi -
ALhas to be 0, soESIhas to be 0. - [0x00401B3D] cmovnz esi, edx -
ESIhas to be 0, soZFhas to be 1. - [0x0014FDB8] cmpxchg bl, dl -
ZFhas to be 1, soALhas to be equal toBL. (LetBLbeX) - [0x00401B14] rol al, cl - This operation must be equal to
BL, i.e.ROL AL, CL = X - [0x0014FDB4] mov cl, [esp+ebx+88h] - Let
CLbeY, i.e.ROL AL, Y = X - [0x0014FDB8] xor al, ah -
ROL (XOR AL, AH), Y = X - [0x0014FDB4] mov ah, [esp+ebx+0B4h] - Let
AHbe Z, i.e.ROL (XOR AL, Z), Y = X - [0x00401A9C] mov al, [eax+ecx] - Let
ALbeIfor Input, i.e.ROL (XOR I, Z), Y = X
Diamonds are forever
I since that's what we need to find:
(I ^ Z) ROL Y = X
=> I ^ Z = X ROR Y
=> I = ( X ROR Y ) ^ Z
Now it's a matter of going through each iteration of the function to gather X, Y and Z. Let's go through the first few together. Remember that for words, rotate operators repeat themselves every 16 (0x10) times. For example ROR AX, 56 = ROR AX, 6 and ROR AX, F3 = ROR AX, 3. So:
+-----------------------+-----------------------------------+-------+
| X | Y | Z | X ROR Y | ( X ROR Y ) ^ Z | I |
+-----------------------+-----------------------------------+-------+
| C3 | 56 | 46 | 0F | 49 | I |
|-------------------------------------------------------------------|
| CC | F5 | 15 | 66 | 73 | s |
|-------------------------------------------------------------------|
| BA | AC | F4 | AB | 5F | _ |
|-------------------------------------------------------------------|
| 4E | 1B | BD | C9 | 74 | t |
+-------------------------------------------------------------------+
| ... | ... | ... | ... | ... | ... |
+-------------------------------------------------------------------+
After what feels like a few years we obtain the e-mail address to advance to the next challenge:
Command Prompt
C:\>you_are_very_good_at_this.exe
I have evolved since the first challenge. You have not. Bring it.
Enter the password> Is_th1s_3v3n_mai_finul_foarm@flare-on.com
You are success
C:\>